REGLAS BÁSICAS DE LA LOGICA DE PREDICADOS
       (Cálculo de Cuantores)
      Proof Checker
      Las Reglas Básicas del Cálculo de Cuantores son 4, una de Introducción y otra de Eliminación por cada uno de los dos Cuantificadores Universal y Particular.
      1. REGLA DE ELIMINACIÓN DEL GENERALIZADOR (EG)
      2. REGLA DE INTRODUCCIÓN DEL GENERALIZADOR (IG)
      3. REGLA DE INTRODUCCIÓN DEL PARTICULARIZADOR (IP)
      4. REGLA DE ELMINACIÓN DEL PARTICULARIZADOR (EP)

      Introducción a Cálculo Cuantores
















































































































































































































































































































      ELIMINACIÓN DEL GENERALIZADOR (EG)
      (Adaptación Lógica Simbólica de M.Garrido)
      1. La Regla de EG permite suprimir el cuantificador "x y cerrar la matriz mediante la introducción de una constante individual.
      2. La Regla de EG tiene su fundamentación en lo siguiente: se considera legítimo en muchos discursos el poder pasar de la ley general al caso concreto, es decir, el deducir el este particular a partir del todos universal.
        En definitiva, se parte de la base de que:
        aquello que verdadero de todos los x, es verdadero tambien de uno cualquiera de tales x
      3. Sabemos que el Cuantificador universal o Generalizador puede ser entendido como una extensión o generalización del Conjuntor. Pues bien, en este contexto, la regla de EG viene a ser como una extensión o generalización de la regla de la Eliminación del Conjuntor (EC), por la que se pasa de la posición de una conjunción a la posición de uno de sus miembros.
      4. El Esquema de la Regla de EG es el siguiente: 
        Todo es material
-----------------
Esto es material
        Su formalización:
        "x Px
        -----------------------------------
        Pa

      EJEMPLO
      Reglas Básicas Cálculo Cuantores





















































































































































































































































































































































      EJEMPLO SOBRE APLICACIÓN REGLA BASICA DE EG
      Argumento: 
      Todo griego es europeo
Todo ateniense es griego
Todo atieniense es europeo
      Formalización del argumento: 
      P=Ateniense.
Q=Griego.
R=Europeo.
      "x (Qx ® Rx); "x (Px ® Qx); |-- "x (Px ® Rx)

      ¿Cómo realizar la Derivación de este argumento mediante el Cálculo de Cuantores?

      Es evidente que, para su derivación, debemos conocer las Reglas Básicas que nos permitan operar. Veamos como se aplica la Regla de la EG.
      Formalización del argumento para su derivación:
      |-- "x (Px ® Rx)

      • -1 "x (Qx ® Rx)
      • -2 "x (Px ® Qx)
      Derivación del Argumento:
      |-- "x (Px ® Rx)
      • -1 "x (Qx ® Rx)
      • -2 "x (Px ® Qx)
      • 3 Pa ® Qa EG 2
      • 4 Qa ® Ra EG 1
      • 5 Pa ® Qa Sil 3,4
      • 6 "x (Px ® Rx) IG 5
      Comentario
      Regla de EG





















































































































































































































































































































































      COMENTARIO A EJEMPLO SOBRE APLICACIÓN REGLA BASICA DE EG
      Derivación del Argumento:
      |-- "x (Px ® Rx)
      • -1 "x (Qx ® Rx)
      • -2 "x (Px ® Qx)
      • 3 Pa ® Qa EG 2
      • 4 Qa ® Ra EG 1
      • 5 Pa ® Qa Sil 3,4
      • 6 "x (Px ® Rx) IG 5
      COMENTARIO

      • Observar sobre todo los pasos 1, 2, 3 y 4. En los supuestos 1 y 2 nos encontramos con enunciados dominados por el cuantificador universal: ["x]
      • En el Paso 3 hemos aplicado la Regla de la EG al supuesto 2. Tal regla nos permite suprimir el Cuantificador universal ["x] y, actuando sobre las matrices (Px y Qx), introducir unas matrices de caracter particular a partir de la base de que lo que es verdad para todos lo es tambien para estos.
      • En definitiva, si el supuesto 2 afirma que todo ateniense es griego. El paso 3 está afirmando que aquel individuo concreto que sea ateniense tambien será griego.
      • En el paso 4 hemos aplicado la Regla de EG al supueso 1. Tal regla nos permite tambien suprimir el Cuantificador universal ["x] y, actúando sobre las matrices (Qx y Rx), introducir matrices de caracter particular a partir de la base de que lo que es verdad para todos lo es tambien para estos.
      • En definitiva, si el supuesto 1 afirma que todos los griegos son europeos. El paso 4 afirma que aquel individuo concreto que sea griego tambien será europeo.
      OTRO EJERCICIO

      Formaliza y aplica la Regla de EG al argumento siguiente: 

                                              
      Todos inglés es europeo                     I=Inglés
Todo Londinense es inglés                   E=Europeo
--------------------------                  L=Londinense
Todo Londinense es europeo

      Si quieres conocer la Solución pulsa AQUÍ
      Ejemplo uso Regla de EG





















































































































































































































































































































































      SOLUCIÓN EJERCICIO SOBRE APLICACIÓN REGLA BASICA DE EG
      Formalización del argumento para su derivación:
      |-- "x (Lx ® Ex)
      • -1 "x (Ix ® Ex)
      • -2 "x (Lx ® Ix)
      Derivación del Argumento:
      |-- "x (Lx ® Ex)
      • -1 "x (Ix ® Ex)
      • -2 "x (Lx ® Ix)
      • 3 La ® Ia EG 2
      • 4 Ia ® Ea EG 1
      • 5 La ® Ea Sil 3,4
      • 6 "x (Lx ® Ex) IG 5
      Comentario uso Regla de EG





















































































































































































































































































































































      INTRODUCCIÓN DEL GENERALIZADOR (IG)
      (Adaptación Lógica Simbólica de M.Garrido)
      1. La Regla de IG permite introducir el cuantificador "x .
      2. Se corresponde con el uso ordinario del principio intuitivo: lo que vale para un caso cualquiera, vale para todos los casos. Dicho principio, por tanto, permite establecer una inferencia que va de cualquiera a todo, es decir, del caso a la ley.
      3. En la argumentación ordinaria pueden encontrarse abundantes ejemplos del uso de este principio intuitivo:cuando un individuo organicamente normal ingiere cierta substancia y ello produce en él cierta reacción, es lógico pensar que esta misma reacción se producirá en todos aquellos que ingieran tal substancia (siempre y cuando, claro está, que el individuo sea en verdad un indiviudo cualquiera, y no, por ejemplo, un individuo que padezca determinadas enfermedades.
      4. El uso de este principio intuitivo tiene lugar, sobre todo, en el terreno de la matemática. Una ilustración del empleo de tal principio lo encontramos en los Elementos de Geometria de Euclides, en donde se encuentra la demostración del famoso teorema según el cual los tres ángulos de un triángulo suman dos rectos.
      5. El paso inferencial de la predicación de una nota respecto de un individuo cualquiera a la atribución de la misma nota respecto de todo indiviudo en general, solamente está justificado si el individuo que sirve de base a la Generalización es un indiviudo absolutamente cualquiera. Solamente teniendo la seguridad de haber elegido a ese individuo, y despues de probar que posee la propiedad deseada, se puede concluir la generalización.
      6. Si trasladamos todo lo dicho al terreno práctico del lenguaje simbólico habría que señalar que será lícito pasar de una predicación Pa a la generalización de la misma, unicamente despues de asegurarse de que el individuo elegido no figura en ningún supuesto o hipótesis sin cancelar de la que dependa la predicación Pa. Si esta condición no se cumple, entonces la generalización será incorrecta.
      7. El Esquema de la Regla de IG es el siguiente:
        Pa
        -----------------------------------
        "x Px
      8. NOTA:En la deducción, Pa no debe figurar en ningún supuesto no cancelado.
      9. Ahora bien, mientras que el paso desde uno cualquiera a todos es un tránsito lógico, no sería lógico pasar de un este, condicionado al cumplimiento de alguna nota predicativa que no sabemos si cumple o no, a todos. Por todo ello, la combinación de las Reglas de EP e IG es fuente de multitud de conflictos en la derivación.

      EJEMPLO
      Reglas Básicas Cálculo Cuantores





















































































































































































































































































































































      REPRESENTACIÓN TEOREMA SEGÚN EL CUAL LOS TRES ANGULOS DE UN TRIANGULO SUMAN DOS RECTOS
       Construyase un triángulo cualquiera y trácese una paralela a la base que pase por el vértice opuesto a ésta. Resultan las siguientes igualdades: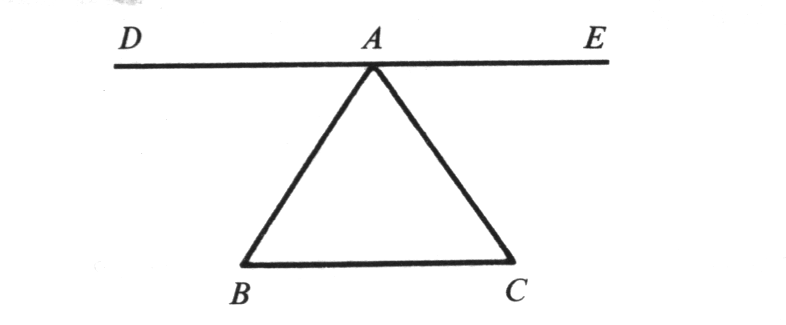 

      DAB=ABC (igualdad de ángulos alternos internos)
EAC=ACB (igualdad de ángulos alternos internos)
DAB + EAC = ABC + ACB (la suma de los primeros miembros
de dos igualdades es igual a la suma de los segundos)
Y añadiendo BAC a cada miembro (según el principio de que 
si se añade una misma cosa a cada miembro de una igualdad 
se vuelve a obtener una igualdad):
DAB + EAC + BAC + = ABC + ACB + BAC
Ahora bien, el primer miembro de la última igualdad vale
dos rectos. Por consiguiente tambien los valdrá el segundo.
Queda demostrado, por tanto que los tres ángulos de un
triángulo  valen dos rectos.
      Esta prueba tiene por base la construcción de una figura o diagrama individual y concreto, y sin embargo permite concluir en general para todo triángulo. La razón es que dicho diagrama, a pesar de ser individual y concreto, es considerado como un diagrama cualquiera. Podía perfectamente haber sido cualquier otro. El caracter enteramente arbitrario de la elección de la figura construida permite la inferencia.
      Introducción Generalizador





















































































































































































































































































































































      CONFLICTOS ENTRE LAS REGLAS EG E IG
      La combinación de las reglas EP e IG, cuya aplicación entraña el cumplimento de una serie de condiciones, puede dar lugar, si se olvida tener en cuenta dichas condiciones, a deducciones inválidas como esta:
      • -1 $Px
      • -2 Pa
      • 3 "x Px IG 2 (?)
      • 4 " Px EP 1,2-3
      Y es que la aplicación de la regla IG en la 3ª linea es ilegítima.
      La razón es la siguiente: según la regla de la IG, el parametro a, que sirve de base a la generalización, ha de representar un individuo absolutamente cualquiera, esto es, no sujeto a ninguna hipótesis; pero el individuo supuesto en la segunda linea no es un individuo cualquiera, sino un individuo tal, esto es, un individuo condicionado al cumplimiento de la nota P.
      Dicho de otro modo: la regla IG no es aplicable a una parámetro hipoteticamente situado bajo el alcance de la regla EP. En caso contrario valdría la inferencia, claramente incorrecta, del enunciado siguiente:

      Algunos hombres son ricos

      Al siguiente enunciado:

      Todos los hombres son ricos
      Regla de IG





















































































































































































































































































































































      EJEMPLOS SOBRE APLICACIÓN REGLA BASICA DE IG
      La necesidad de andarse con cuidado en la aplicación de la regla del IG, es algo que puede comprobarse mediante el ensayo de derivación formal de los dos argumentos siguientes, el primero de los cuales es correcto y el segundo no.

      ARGUMENTO PRIMERO 
      O todos son negros o todos son amarillos; por consiguiente,
todos son o negros o amarillos
      FORMALIZACIÓN PRIMER ARGUMENTO: 
      P=negro
Q=amarillo
      "x (Px Ú "x Qx) |-- "x (Px Ú Qx)

      ¿Cómo realizar la Derivación del Primer argumento mediante el Cálculo de Cuantores?

      Es evidente que, para su derivación, debemos conocer las Reglas Básicas que nos permitan operar. Veamos como se aplica la Regla de la IG.
      Formalización del argumento para su derivación:
      |-- "x (Px Ú Qx)

      • -1 "x (Px Ú "x Qx)
      Derivación del primer Argumento:
      |-- "x (Px Ú Qx)
      • -1 "x (Px Ú "x Qx)
      • 2 "x Px [Premisa subsidaria]
      • 3 Pa EG 2
      • 4 Pa v Qa ID 3
      • 5 "x Qx [Premisa subsidaria]
      • 6 Qa EG 5
      • 7 Pa v Qa ID 6
      • 8 Pa v Qa Cas 1, 2-4, 5-7
      • 9 "x (Px Ú Qx) IG 8

      SEGUNDO ARGUMENTO 
      Todos son o negros o amarillos; por consiguiente,
o todos son negros o todos son amarillos
      FORMALIZACIÓN: 
      P=negro
Q=amarillo
      "x (Px Ú Qx) --| "x (Px Ú "x Qx)

      ¿Cómo realizar la Derivación del Segundo argumento mediante el Cálculo de Cuantores?

      Es evidente que, para su derivación, debemos conocer las Reglas Básicas que nos permitan operar. Veamos como se aplica la Regla de la IG.
      Formalización del 2º argumento para su derivación:
      |-- "x (Px Ú "x Qx)

      • -1 "x (Px Ú Qx)
      Derivación del 2º Argumento:
      |-- "x (Px Ú "x Qx)
      • -1 "x (Px Ú Qx)
      • 2 Pa v Qa EG 1
      • 3 Pa Premisa subsidiaria
      • 4 "x Px ?
      Comentario
      Regla de IG





















































































































































































































































































































































      COMENTARIO A EJEMPLOS SOBRE APLICACIÓN REGLA BASICA DE IG
      Derivación del primer Argumento:
      |-- "x (Px Ú Qx)
      • -1 "x (Px Ú "x Qx)
      • 2 "x Px [Premisa subsidaria]
      • 3 Pa EG 2
      • 4 Pa v Qa ID 3
      • 5 "x Qx [Premisa subsidaria]
      • 6 Qa EG 5
      • 7 Pa v Qa ID 6
      • 8 Pa v Qa Cas 1, 2-4, 5-7
      • 9 "x (Px Ú Qx) IG 8
      COMENTARIO

      Observar que en el primer argumento la regal de IG se aplica a la linea 8 (resultado de una prueba por casos que es ya independiente de supuestos subsidiarios sin cerrar). En este sentido, por tanto, en la linea 9 es correcta la aplicación del IG.

      Derivación del 2º Argumento:
      |-- "x (Px Ú "x Qx)

      • -1 "x (Px Ú Qx)
      • 2 Pa v Qa EG 1
      • 3 Pa Premisa subsidiaria
      • 4 "x Px ?
      COMENTARIO

      En este argumento no sería correcto aplicar la regla de IG a la linea 3 para construir la linea 4. Y es que en la linea 3 nos encontramos con un supuesto meramente subsidiario y sin cerrar.

      Ejemplos uso Regla de IG





















































































































































































































































































































































      INTRODUCCIÓN AL PARTICULARIZADOR (IP)
      (Lo que es verdadero de uno es verdadero de alguien) (Adaptación Lógica Simbólica de M.Garrido)
      1. La Regla de IP permite introducir el cuantificador $x .
      2. Se corresponde con el uso ordinario del principio intuitivo que nos permite entender que es posible pasar de la atribución de una nota determinada en un individuo a la afirmación de que existe alguien (al menos uno) que posee tal nota.
      3. En definitiva, el uso de esta regla implica el paso lógico que va de la afirmación de este a la afirmación de alguno. Por ejemplo, es lógico deducir de esto arde que algo arde o de que esto es material que algo es material.
      4. El Esquema de la Regla de IP es el siguiente:
        Pa
        -----------------------------------
        $x Px

      EJEMPLO
      Reglas Básicas Cálculo Cuantores





















































































































































































































































































































































      EJEMPLO SOBRE APLICACIÓN REGLA BASICA DE IP
      $x (Px ® Qx); Pa; |-- $x Qx

      ¿Cómo realizar la Derivación de este argumento mediante el Cálculo de Cuantores?

      Es evidente que, para su derivación, debemos conocer las Reglas Básicas que nos permitan operar. Veamos como se aplica la Regla de la IP.
      Formalización del argumento para su derivación:
      |-- $x (Qx)

      • -1 "x (Px ® Qx)
      • -2 Pa
      Derivación del Argumento:
      |-- "x (Qx)
      • -1 "x (Px ® Qx)
      • -2 Pa
      • 3 Pa ® Qa EG 1
      • 4 Qa MP 3,2
      • 5 $x (Qx) IP 4
      Comentario
      Regla de IP





















































































































































































































































































































































      COMENTARIO A EJEMPLO SOBRE APLICACIÓN REGLA BASICA DE IP
      Derivación del Argumento:
      |-- "x (Qx)
      • -1 "x (Px ® Qx)
      • -2 Pa
      • 3 Pa ® Qa EG 1
      • 4 Qa MP 3,2
      • 5 $x (Qx) IP 4
      COMENTARIO

      • Observar que despues de la aplicación a la linea 1 de la Regla de EG en la linea 3, se forma una condicional cuyo antecedente se encuentra tambien en la linea 2. Ello nos permite conseguir en la linea 4, Qa, mediante la aplicación de la regla del MP, a la lineas 3,2.
      • Sobre la linea 4 y Qa, aplicamos ahora la regla de Introducción del Particularizador (IP) que es lo que necesitamos para llegar a la conclusión. Eso lo hacemos en la linea 5.
      Ejemplo uso Regla de IP





















































































































































































































































































































































      ELIMINACIÓN DEL PARTICULARIZADOR (EP)
      (Adaptación Lógica Simbólica de M.Garrido)
      1. La Regla de EP permite eliminar el cuantificador $x .
      2. Por un principio de Simetría podríamos pensar que dado que la regla de la eliminación del generalizador (EG) o cuantificador universal tiene la forma:

        "x
        ---------------------------------------
        Pa
        la Regla de la eliminación del particularizador (EP) debería tener esta:

        $x
        ---------------------------------------
        Pa
      3. Pues nada más lejos de la realidad. Y es que nada más facil que inferir un enunciado falso a partir de un enunciado verdadero mediante esta regla. Supongamos que alguien razonara así: 
        Algún griego del siglo IV escribió la Etica a Nicómaco
Epicuro escribió la Etica a Nicómaco
        Es evidente que de un enunciado particular verdadero, se concluye otro que es absolutamente falso.
      4. Es imposible, por tanto, justificar, desde un punto de vista lógico, el paso de una premisa como: 
        Hay algún x tal que x es P
        A otra del tipo: 
        a es P
      5. Ahora bien, tanto en la Argumentación natural como en el razonamiento científico se aplica un patrón de inferencia que de algún modo cabría calificar de Regla de Eliminación del cuantificador particular. Ello sucede cuando se razona así: 
        Alguien roba un cuadro de Vermeer
[$x](Px)
Supongamos que ha sido Morgan [Pa]
Ahora bien, todo lo que Morgan roba se lo vende a Rin
Además Rin abastece de cuadros robados a Tirps
Deberíamos hacer una visita a Tirps[X]
------------------------------------------------------------
Tirps debe tener el cuadro de Vermeer[X]
      6. Por tanto, el Esquema de la Regla de EP es el siguiente: El punto de partida tiene que ser una proposición particular. De ella, consideramos como hipótesis provisional un parametro individual (Pa). A partir de ahí hay que emprender una suderivación que se abra con Pa con el objeto de llegar a la conclusión deseada. Si llegamos a tal conclusión, podríamos cerrar la suderivación, que debe presentar el siguiente esquema:

        $x
        Pa
        .
        .
        .
        .
        X
        -----
        X [EP]
      7. El parametro que abrimos provisionalmente tiene el requisito siguiente: hemos visto como en el caso de la regla de la EG, el requisito del parametro sobre el que se efectuaba la generalización era que representara a un individuo cualquiera . Pues bien, ahora en la Regla de la Eliminación del Particularizador (EP), el requisito es inverso: al decir supongamos que a es ese inviduo que es P , estamos haciendo de a un caso especial y diferente.
      8. Pues bien, ello exige respetar una serie de Condiciones dentro de la derivación:
        • El símbolo individual no debe aparecer en la premisa existencial de la que se parte.
        • La linea terminal o conclusión no debe contener tampoco ese símbolo individual, ni depender de ningúna premisa no descargada que la contenga.
      9. Nota: La combinación de las Reglas de EP e IG es fuente de multitud de conflictos en la derivación.

      EJEMPLO
      Reglas Básicas Cálculo Cuantores





















































































































































































































































































































































      CONFLICTOS ENTRE LAS REGLAS EG E IG
      La combinación de las reglas EP e IG, cuya aplicación entraña el cumplimento de una serie de condiciones, puede dar lugar, si se olvida tener en cuenta dichas condiciones, a deducciones inválidas como esta:
      • -1 $Px
      • -2 Pa
      • 3 "x Px IG 2 (?)
      • 4 " Px EP 1,2-3
      Y es que la aplicación de la regla IG en la 3ª linea es ilegítima.
      La razón es la siguiente: según la regla de la IG, el parametro a, que sirve de base a la generalización, ha de representar un individuo absolutamente cualquiera, esto es, no sujeto a ninguna hipótesis; pero el individuo supuesto en la segunda linea no es un individuo cualquiera, sino un individuo tal, esto es, un individuo condicionado al cumplimiento de la nota P.
      Dicho de otro modo: la regla IG no es aplicable a una parámetro hipoteticamente situado bajo el alcance de la regla EP. En caso contrario valdría la inferencia, claramente incorrecta, del enunciado siguiente:

      Algunos hombres son ricos

      Al siguiente enunciado:

      Todos los hombres son ricos
      Regla de EP





















































































































































































































































































































































      EJEMPLO SOBRE APLICACIÓN REGLA BASICA DE EP
      "x (Px ® Qx); $x (Rx Ù Px); |-- $x (Rx Ù Qx)

      ¿Cómo realizar la Derivación de este argumento mediante el Cálculo de Cuantores?

      Es evidente que, para su derivación, debemos conocer las Reglas Básicas que nos permitan operar. Veamos como se aplica la Regla de la EP.
      Formalización del argumento para su derivación:
      |-- $x (Rx Ù Qx)

      • -1 "x (Px ® Qx)
      • -2$x (Rx Ù Px)
      Derivación del Argumento:
      |-- $x (Rx Ù Qx)
      • -1 $x (Px ® Qx)
      • -2$x (Rx Ù Px)
      • 3 Pa ® Qa EG 1
      • 4 Ra Ù Pa
      • 5 Pa EC 4
      • 6 Qa MP 2,5
      • 7 Ra EC 4
      • 8 Ra Ù Qa
      • 9 $x (Rx Ù Qx) IP 8
      • 10 $x (Rx Ù Qx) EP 2, 4-9

      Comentario
      Regla de EP





















































































































































































































































































































































      COMENTARIO A EJEMPLO SOBRE APLICACIÓN REGLA BASICA DE EP
      Derivación del Argumento:
      |-- $x (Rx Ù Qx)
      • -1 "x (Px ® Qx)
      • -2$x (Rx Ù Px)
      • 3 Pa ® Qa EG 1
      • 4 Ra Ù Pa
      • 5 Pa EC 4
      • 6 Qa MP 2,5
      • 7 Ra EC 4
      • 8 Ra Ù Qa
      • 9 $x (Rx Ù Qx) IP 8
      • 10 $x (Rx Ù Qx) EP 2, 4-9

      COMENTARIO

      • En la linea 3 hemos eliminado sin problemas el cuantificador universal.
      • En la linea 4 eliminamos el cuantificador particular que aparece en 2. Ahora bien, al hacerlo tenemos que colocarlo hipótesis subsidaria y, a partir de ahí, iniciar una subderivación que nos debería llevar a la conclusión deseada. Unicamente, en ese caso, podríamos usar realmente de la Regla EP
      • En las lineas 5,6,7,8 usamos las reglas del cálculo de juntores.
      • En la linea 9 podemos usar la regla de la Introducción del Particularizador (IP) a partir de la base de que lo es verdad de uno lo es tambien de alguno. Notar tambien que esta linea coincide con la conclusión que buscamos.
      • En la linea 10, despues de situar de nuevo la conclusión a la que hemos llegado, señalamos que para alcanzarla usamos la Regla de EP aplicada a la lineas 2, 4-9.
      OTRO EJERCICIO

      Formaliza y aplica la Regla de EG al argumento siguiente: 

                                              
      Ningún hombre tiene alas                     P=Ser Hombre
Algún ser vivo es hombre                     Q=Tener alas
--------------------------                   R=Ser vivo
Algún ser vivo no tiene alas

      Si quieres conocer la Solución pulsa AQUÍ
      Ejemplo uso Regla de EP





















































































































































































































































































































































      SOLUCIÓN EJERCICIO SOBRE APLICACIÓN REGLA BASICA DE EP
      Formalización del argumento para su derivación:
      |-- $x (Rx Ù ¬ Qx)
      • -1 "x (Px ® ¬ Qx)
      • -2 $x (Rx Ù Px)
      Derivación del Argumento:
      |-- $x (Rx Ù ¬ Qx)
      • -1 "x (Px ® ¬ Qx)
      • -2 $x (Rx Ù Px)
      • 3 Pa ® ¬ Qa EG 1
      • 4 Ra Ù Pa
      • 5 Pa EC 3
      • 6 ¬ Qa MP 3,5
      • 7 Ra EC 4
      • 8 Ra Ù ¬ Qa IC 7 , 6
      • 9 $x (Rx Ù ¬ Qx) IP 8
      • 10 $x (Rx Ù ¬ Qx) EP 3, 3-9

      Comentario uso Regla de EP