En el estudio de las proposiciones categóricas se ha visto como sus Términos se refieren a nombres comunes (hombre, animal, cuadrupedo) que no denotan a un individuo particular sino a un Conjunto o Clase de individuos. Además, las relaciones que pueden establecerse entres tales términos puede ser de inclusión o exclusión total (universal) o parcial (particular) de un conjunto en otro.

TODOS LOS HOMBRES SON MORTALES                  MaP
TODOS LOS AFRICANOS SON HOMBRES                 SaM
-----------------------------------           --------
TODOS LOS AFRICANOS SON MORTALES                SaP  (Inclusión total)

NINGÚN AFRICANO ES EUROPEO                      MeP
TODOS LOS ARGELINOS SON AFRICANOS               SaM  
-----------------------------------           --------
NINGÚN ARGELINO ES EUROPEO                      SeP  (Exclusión total) 

TODO MAMÍFERO ES VERTEBRADO                     MaP
ALGÚN ANIMAL ES MAMÍFERO                        SiM
-----------------------------------           ---------
ALGÚN ANIMAL ES VERTEBRADO                      SiP   (Inclusión parcial)

Estos ejemplos, están relacionados con el modo de relacionarse los términos, por inclusión o exclusión, dentro de la Silogística Tradicional. Ahora, veremos como puede analizarse esto mismo aunque a nivel de Diagramas.
En el siglo XVIII, Euler utilizó círculos para expresar de modo gráfico las relaciones entre los términos. En la actualidad, sin embargo, se han impuesto, por sus ventajas los Diagramas del lógico inglés JOHN VENN (1834-1923), el cual se inspiró en el cálculo de clases de Boole.

1. Un Círculo pequeño dentro de otro círculo mayor sería la imagen normal de TODO S es P. Y es que en una proposición universal afirmativa, lo normal es que la extensión del predicado sea mayor que la extensión del sujeto, como cuando decimos: Todo triángulo es una figura. De todos modos, la presentación gráfica de Euler sobre las proposiciones universales afirmativas, presenta problemas que los diagramas de Venn solucionan mejor.
2. Mediante la presentación de dos Círculos separados, uno representando S en la proposición y otro P de tal proposición, se intentaba señalar que nada tenían que ver el uno con el otro y así expresar las proposiciones universales negativas del tipo NINGÚN S es P.
3. Mediante la intersección de dos círculos, Euler representaba las proposiciones particulares. Con el objeto de expresar una proposición particular afirmativa del tipo ALGÚN S es P; S-P se encontraban en la zona de intersección.
4. Con el objeto de expresar una proposición particular negativa, del tipo Algún S no es P; S-P se encuentran separados cada uno en la zona de no intersección.

---

---

---

---

---

---

---

---

VENTAJAS DE LOS DIAGRAMAS DE VENN

---

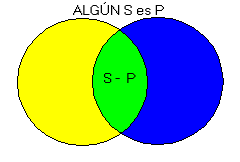
Los Diagramas de Venn representan, del mismo modo que los de Euler, la extensión de los términos mediante círculos, y mediante la intersección de círculos. Pero tienen la ventaja de especificar además si la clase de la que se trate es o no vacía.
Un Conjunto o Clase es vacía cuando carece realmente de individuos, como sucede, por ejemplo, con el conjunto de los círculos cuadrados o de los hombres de piel azul, y no es vacía en caso contrario.
La representación gráfica de los tres tipos de clases: Clase no vacía, Clase vacía y Clase de la que no sabemos realmente si es vacía o no, (Clase neutra) es la siguiente:

---

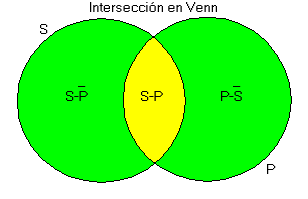
Por otra parte, en los Diagramas de Venn, la Intersección de dos Círculos representativos de ambas Clases o Conjuntos, puede ser mejor aprovechada si se distingue en ella de un modo más explícito y sistemático la zona de intersección, compartida por los individuos de ambos, de las zonas de no intersección, privativas de los individuos de cada uno. Así por ejemplo, en la figura siguiente:

---